为了在使用上方便,对某些概念进行定义时,总会给上更多的限制条件。这样一来,在验证某些概念时就需要验证更多条件,这显然不是我们想要的。但通过下文的证明,这多余的条件其实更加方便使用。本文讨论的是,线性空间八大公理与七大公理等价的问题。目的就是为了说明上面的事实,引导学生学会读书。 综上事实一即得证. (事实二) 基于上面两个事实,下面证明下面的命题:
在郭聿琦等主编的《线性代数带引》,或者说任何一本代数学教材,在定义线性空间时均采用了如下的八大公理:

但是笔者在学习过程中发现,从本质上讲,八大公理只需七大公理即可,第一公理可由后七公理导出。本文正是为证明此命题的。
首先证明两个事实:
事实一、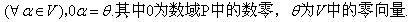
事实二、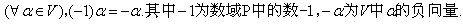
说明:为了避免在命题证明过程中出现循环引用的情况,下面的推导过程前后步骤间均给出直接引用的事实,用记号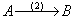 表示这一原则,其中的
表示这一原则,其中的 表示利用公理(2)可由得到。
表示利用公理(2)可由得到。
证明:
(事实一)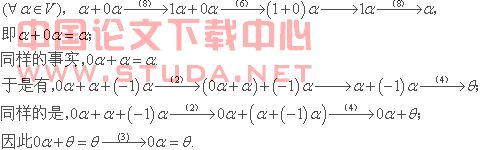

命题:线性空间中八大公理(1)(2)(3)(4)(5)(6)(7)(8)与七大公理(2)(3)(4)(5)(6)(7)(8)等价。
可以看出,两大公理体系仅有一个公理的差别,因此为证明此命题只需要公理(1)可以由其余七大公理导出即可。
证明:必要性是显然成立的;
充分性
只需证明(1)可由(2)(3)(4)(5)(6)(7)(8)推出即可。
综上全部,命题即得以证明。
可以看出,上面两个定义的等价性是毋庸质疑的;并且可以看出,在证明的过程中只是反复的引用公理事实。这就启示我们在定义概念时,多加条件其实没有影响,相反还会简化我们验证的过程,否则每次都要重复上面的过程去验证交换律,这就是公理化体系的优点。
这个命题是由我的恩师王正攀转述给我们的,他得之于郭聿琦教授。
参考文献
[1]郭聿琦.岑嘉评.徐贵桐.线性代数导引[M].北京:科学出版社,2001.
关于线性空间定义的一点注记
来源::未知 | 作者:水晶宫足球俱乐部_欧宝体育APP官方下载-直播|平台 | 本文已影响 人
- 上一篇:函数概念教学的几点思考
- 下一篇:求解不可微函数优化的一种混合遗传算法
随机阅读
- [数学] 函数概念教学的几点思考
- [数学] 构造法在高等代数中的应用
- [数学] 康托尔与集合论
- [数学] 试论数学课堂教学中教师的
- [数学] 基于区分链表的属性约简改
- [数学] 求解不可微函数优化的一种
- [数学] 关于二面角的平面角定位分
- [数学] 三对角系统并行算法的研究
- [数学] 立体几何中二面角的平面角
- [数学] 数学教学中如何体现学生的
- [数学] 函数图象中体现的辩证观点
- [数学] 加强数学实验教学 推进新
- [数学] 构造法在高等代数中的应用
- [数学] 有关抽象函数的全面探析
- [数学] 康托尔与集合论
- [数学] 数学课堂探究性学习问题设
- [数学] “等”对“不等”的启示
- [数学] 三对角系统并行算法的研究
- [数学] 计数查找算法的研究
- [数学] 浅谈数学导入教学策略
- [数学] 数学学习中的联结及导向策
- [数学] 关于数学教学生活化的点滴
- [数学] 关于线性空间定义的一点注
- [数学] 关于二面角的平面角定位分
- [数学] 基于区分链表的属性约简改
- [数学] 立体几何中二面角的平面角





